
Από τον Θανάση Εγγλέζο Μηχανολόγο Μηχανικό Μελετητή – σχεδιαστή καλουπιών
Κατά την μορφοποίηση των πλαστικών αντικειμένων με τη μέθοδο της έγχυσης, το πολυμερές πρέπει να διανύσει κάποια συγκεκριμένη απόσταση ώστε να επιτευχθεί η πλήρωση της κοιλότητας. Προκειμένου η παραγωγή να είναι αποδοτική, είναι πολύ σημαντικό να καλύπτονται οι γεωμετρικές και διαστασιακές απαιτήσεις του εξαρτήματος, εγχύοντας την μικρότερη ποσότητα πλαστικού και χρησιμοποιώντας την πρέσα με το κατάλληλο μέγεθος. Για να συμβούν τα παραπάνω, οι συνθήκες λειτουργίας και έγχυσης του καλουπιού και της πρέσας πρέπει να βρίσκονται εντός των ορίων που προδιαγράφει ο παραγωγός της πρώτης ύλης. Οι συνθήκες αυτές (πίεση και θερμοκρασία του λειωμένου υλικού, ταχύτητα και χρόνος έγχυσης, θερμοκρασία ψυκτικού μέσου, είδος του θερμοπλαστικού που εγχύεται κ.α.) προσδιορίζουν την «συμπεριφορά» του πλαστικού εντός της κοιλότητας του καλουπιού. Μία παράμετρος που μπορεί να περιγράψει τη «συμπεριφορά» αυτή είναι ο λόγος μήκους ροής του πολυμερούς ως προς το πάχος τοιχώματος του αντικειμένου. Το μήκος ροής αναφέρεται στη διαδρομή που πρέπει να διανύσει το λειωμένο πλαστικό από την πύλη τροφοδοσίας μέχρι την πιο απομακρυσμένη περιοχή του εξαρτήματος, ενώ σαν πάχος ορίζεται το ονομαστικό πάχος του αντικειμένου.
Ως παράδειγμα έχουμε τη διαμόρφωση ενός δοκιμίου (μίας απλής λωρίδας) μήκους 200 χιλιοστών με πάχος 2 χιλιοστά (εικ. 1). Με βάση την παραπάνω περιγραφή, η αναλογία θα είναι 200/2=100. Αυτό μας δείχνει πως ο λόγος ροής προς πάχος του πλαστικού είναι 100:1. Στη συνέχεια αν μειώσουμε το πάχος του δοκιμίου από 2 σε 1 χιλιοστό, τότε ο αντίστοιχος λόγος γίνεται 200/1=200. Συνεπώς, ο λόγος ροής προς πάχος του πλαστικού αυξήθηκε σε 200:1 που σημαίνει πως οι απαιτήσεις έγχυσης για την πλήρωση του τεμαχίου αυξάνονται αναλόγως.
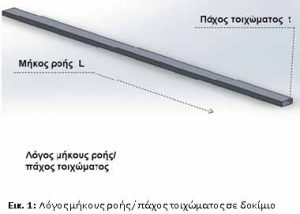
Αναλύοντας την κατάσταση από την πλευρά του χειριστή της πρέσας, το παραπάνω παράδειγμα δείχνει πως η απαραίτητη πίεση για τη διαμόρφωση του αντικειμένου με αναλογία 100:1, δεν είναι πλέον αρκετή αν αλλάξουμε το πάχος και η αναλογία γίνει 200:1. Αντιστοίχως ο χρόνος έγχυσης πρέπει να μειωθεί. Αυτό συμβαίνει λόγω της πτώσης πίεσης που εμφανίζεται από την μείωση της διατομής καθώς και εξ’ αιτίας του ρυθμού με τον οποίο ψύχεται το πλαστικό κατά την επαφή του με τα τοιχώματα του καλουπιού.
Σε γενικές γραμμές μπορούμε να κατατάξουμε τον λόγο ροής προς πάχος σε 3 κατηγορίες:

Στην περίπτωση όπου ο λόγος ροής/πάχος είναι μικρότερος του 100:1 βρισκόμαστε στην κανονική περιοχή έγχυσης. Αυτό σημαίνει πως οι ρυθμίσεις πίεσης και κλειστικού της πρέσας ακολουθούν τις γενικές οδηγίες του παραγωγού της πρώτης ύλης. Αυτή είναι η πλέον εύκολη και συνηθισμένη περίπτωση.
Όταν ο λόγος ροής/πάχος των αντικειμένων βρίσκεται μεταξύ του 100:1 και του 200:1 τότε πλέον οι συνθήκες γίνονται πιο απαιτητικές. Σ’ αυτές τις περιπτώσεις συνήθως επιλέγονται οι μέγιστες ρυθμίσεις (πίεση, ταχύτητα κ.λ.π.) που προτείνει ο προμηθευτής της πρώτης ύλης. Σε ορισμένες μάλιστα περιπτώσεις οι ρυθμίσεις μπορεί να υπερβούν τις προτεινόμενες. Παραδείγματα τέτοιων εφαρμογών αποτελούν αντικείμενα κατασκευασμένα από πολυκαρβονικό (PC), ακρυλικό (PMMA, SAN), ή πολυβυνιλοχλωρίδιο (PVC) των οποίων ο λόγος ροής προς πάχος αντικειμένου πλησιάζει προς το 200:1 ολοένα και μεγαλύτερες πιέσεις χρειάζονται.
Σε εφαρμογές όπου ο λόγος ροής/πάχος των εξαρτημάτων λαμβάνει τιμές μεγαλύτερες του 200:1 τότε πλέον βρισκόμαστε στην περιοχή των λεπτότοιχων εξαρτημάτων όπου όλες οι ρυθμίσεις της μηχανής καθώς και οι υπολογισμοί διαστασιολόγησης του καλουπιού γίνονται με διαφορετικό τρόπο. Σ’ αυτές τις περιπτώσεις η θερμοκρασία του υλικού, η πίεση και η ταχύτητα έγχυσης λαμβάνουν υψηλότερες τιμές. Η μελέτη, η σχεδίαση και κατασκευή του καλουπιού χρειάζεται να αξιολογηθούν ως προς τα υλικά και τις διαστάσεις τους έναντι των σημαντικά αυξημένων φορτίων που θα δεχτούν. Παραδείγματος χάριν, ενώ για την έγχυση απλών εξαρτημάτων η δύναμη κλειστικού της πρέσας είναι της τάξης των 400-450 κιλών ανά τετραγωνικό εκατοστό προβαλλόμενης επιφάνειας, για την έγχυση λεπτότοιχων εξαρτημάτων η αντίστοιχη δύναμη είναι δυνατόν να φτάσει ή ακόμα και να υπερβεί τα 1.000 κιλά ανά τετραγωνικό εκατοστό!
Η κατανόηση της σημασίας του λόγου ροής προς το πάχος του αντικειμένου για το καλούπι και τη διαδικασία παραγωγής είναι ιδιαίτερη για την αντιμετώπιση προβλημάτων έγχυσης. Είναι η σχέση του λόγου ροής προς πάχος με τη κίνηση του πλαστικού μέσα στην κοιλότητα και την γεωμετρία που την προσδιορίζει. Που σημαίνει πως κατά τη διαστασιολόγηση του καλουπιού πρέπει να συνυπολογιστεί η γεωμετρία του εξαρτήματος και η θέση τροφοδοσίας του. Μπορεί παραδείγματος χάριν κάποιος να υπολογίσει την προβαλλόμενη επιφάνεια του εξαρτήματος και να συμπεράνει πως χρειάζονται 400 κιλά ανά τετραγωνικό εκατοστό για το κλειστικό της μηχανής. Μη έχοντας λάβει υπ’ όψιν του το πάχος του αντικειμένου είναι αδύνατον να ολοκληρώσει την πλήρωση της κοιλότητας. Για να την πετύχει ίσως χρειαστούν περισσότερα από 700 κιλά ανά τετραγωνικό εκατοστό ώστε να συμψηφίσει τη διαφορά που προκύπτει από τη γεωμετρία.
Ως δεύτερο παράδειγμα μπορούν να χρησιμοποιηθούν δύο αντικείμενα πάχους 2 χιλιοστών και 1 χιλιοστού αντίστοιχα. Καθώς το υλικό αρχίζει να στερεοποιείται στα μισά της διαδρομής, η πλήρωση πρέπει να γίνει με μεγαλύτερη ταχύτητα (για το λεπτότερο αντικείμενο). Ακολούθως απαιτείται μεγαλύτερη πίεση έγχυσης για να υπερνικήσει το ιξώδες του πολυμερούς, αλλά και την πτώση πίεσης λόγω μικρότερης διατομής. Συνέπεια των παραπάνω είναι πως το πλαστικό εντός της μορφής με το μικρότερο πάχος φορτίζεται με μεγαλύτερη πίεση και προσπαθεί να διαρρεύσει από οποιοδήποτε διαθέσιμο διάκενο (δημιουργώντας φλας) εκτός και αν εφαρμοστεί μεγαλύτερη δύναμης συγκράτησης (κλειστικό).

Ένα τελευταίο παράδειγμα αποτελούν τα λεπτότοιχα εξαρτήματα μίας χρήσης. Σ’ αυτά τα εξαρτήματα ο χρόνος της δεύτερης πίεσης (σιδερώματος) είναι σχεδόν μηδαμινός καθώς διατηρείται μόνο μέχρι να σφραγίσει η πύλη. Τέτοιου τύπου αντικείμενα λόγω του πολύ μεγάλου λόγου ροής προς πάχος τοιχώματος δεν έχουν πολλά περιθώρια συμψηφισμού της συρρίκνωσης, συνεπώς πλήρωση και σιδέρωμα γίνονται σχεδόν ταυτόχρονα.
Ο λόγος ροής προς πάχος είναι συγκεκριμένος για κάθε τύπο υλικού και σχετίζεται εκτός των άλλων και με το ονομαστικό πάχος του αντικειμένου. Βασιζόμενος κάποιος στην εμπειρική γνώση μπορεί να εκτιμήσει αρκετά καλά την απόδοση ενός πλαστικού, ωστόσο εξ’ αιτίας των πολλών παραγόντων που αλληλεπιδρούν συμπεριλαμβανομένης και της γεωμετρίας μπορεί να εμφανιστούν αποκλίσεις. Για έναν πιο ακριβή προσδιορισμό του λόγου, συχνά χρησιμοποιείται μια απλή αλλά αποτελεσματική μέθοδος: το τεστ της σπειροειδούς ροής (εικ. 2). Στην πλέον απλή μορφή του, το τεστ αυτό αποτελείται από ένα καλούπι με σπειροειδή μορφή στο οποίο εγχύεται το πολυμερές. Συνήθως, τρεις παράμετροι διατηρούνται σταθερές, ενώ μεταβάλλεται η τέταρτη. Έτσι για παράδειγμα, το πάχος τοιχώματος, η θερμοκρασία καλουπιού καθώς και η πίεση έγχυσης διατηρούνται σταθερές, ενώ αλλάζει το υλικό έγχυσης. Μ’ αυτόν τον τρόπο παράγονται δείγματα ροής (εικ. 3) από τα εξεταζόμενα θερμοπλαστικά, το «μήκος» των οποίων προσδιορίζει την αναλογία ροής προς πάχος.

Σε περίπτωση που τα παραπάνω δεν επαρκούν και η ακρίβεια της εφαρμογής το απαιτεί, η πλέον ενδεδειγμένη μέθοδος είναι η ανάλυση ροής (εικ. 4)
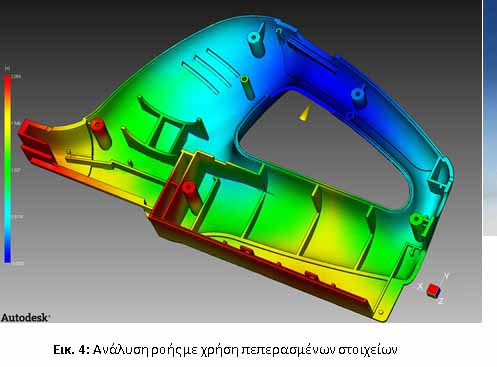
με χρήση κάποιου συστήματος ανάλυσης πεπερασμένων στοιχείων και υπολογιστικής μηχανικής ρευστών (CAE). Κατά την εφαρμογή της μεθόδου αυτής, το εξεταζόμενο μοντέλο αναλύεται, «τεμαχίζεται» σε πολύ μικρά τρίγωνα ή τετράεδρα (αναλόγως αν γίνεται 2Δ ή 3Δ ανάλυση ροής) και ακολούθως εφαρμόζονται ρεολογικοί αλγόριθμοι πάνω σε κάθε τρίγωνο ή τετράεδρο. Γίνεται αμέσως κατανοητό πως ο όγκος των υπολογισμών είναι τεράστιος. Στη συνέχεια τα αποτελέσματα των πράξεων απεικονίζονται με βάση κάποια χρωματική κλίμακα ώστε να είναι πιο εύκολη η εξαγωγή συμπερασμάτων. Η μέθοδος αυτή γίνεται ολοένα και πιο προσιτή καθώς αυξάνεται η υπολογιστική ισχύς των επεξεργαστών και εξελίσσονται οι αλγόριθμοι ανάλυσης.
Από τον
Θανάση Εγγλέζο
Μηχανολόγο Μηχανικό Μελετητή – σχεδιαστή καλουπιών